In this post, we’re going to explore OOP in R as implemented by the R6 package. This post is part 1 of 2, and the end goal is to create an animated fractal tree with R6 & gganimate. Today, we will be creating a static plot of a fractal tree and a series of R6Class objects to help get us there.

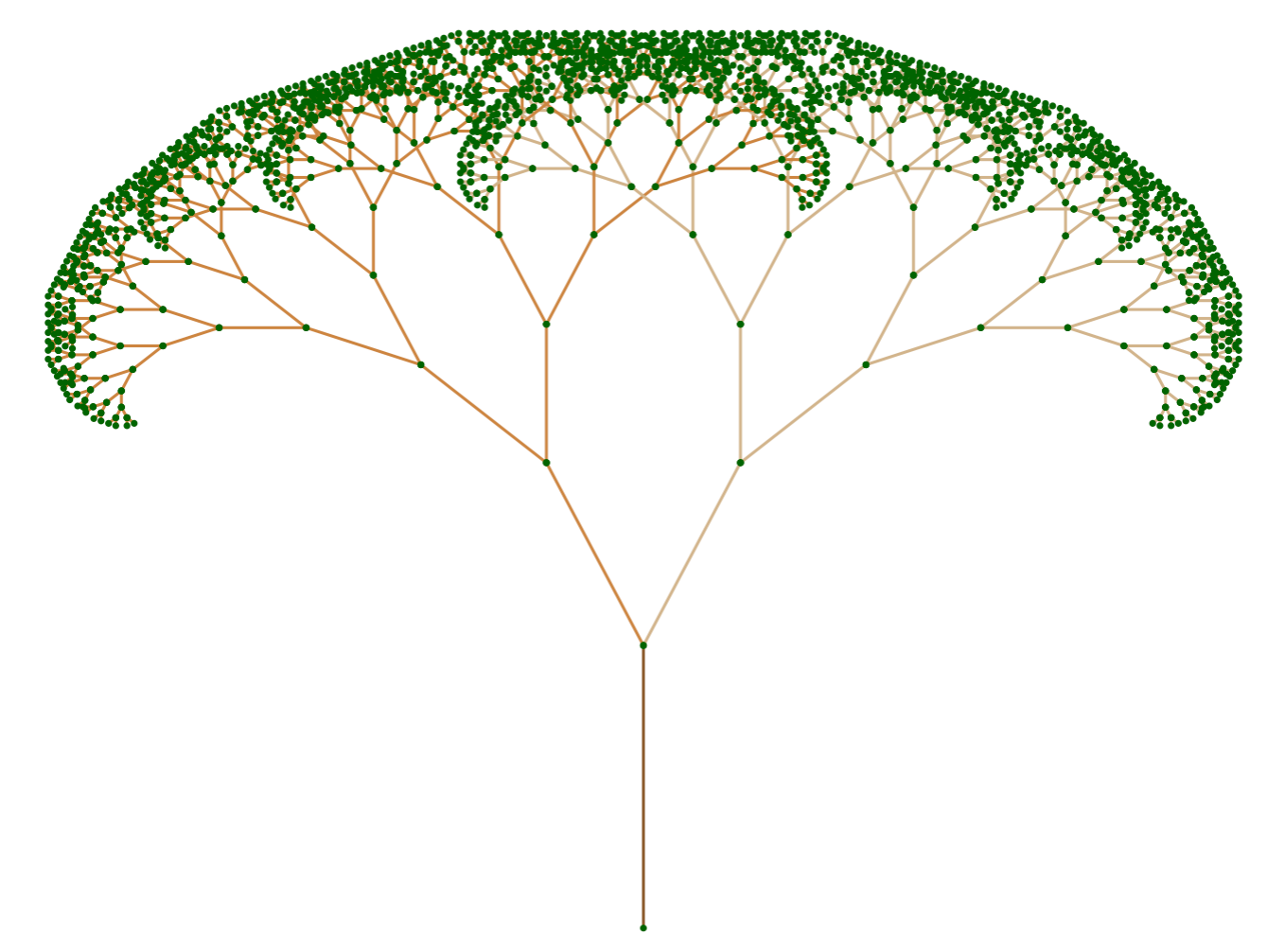
The below code and plot show where we’re going to get by the end of this post.

# Create & plot R6 tree object
tree = fractal_tree$new()
tree$plot()

Note: This post is meant to explore R6 functionality; it’s not claiming to be the best way to create our fractal trees. Some design choices were solely to leverage varied features. Additionally, this post is more example-based than explanation based. For more in-depth explanations, I recomend going to this page from R6 or check out this chapter from Advanced R

Design

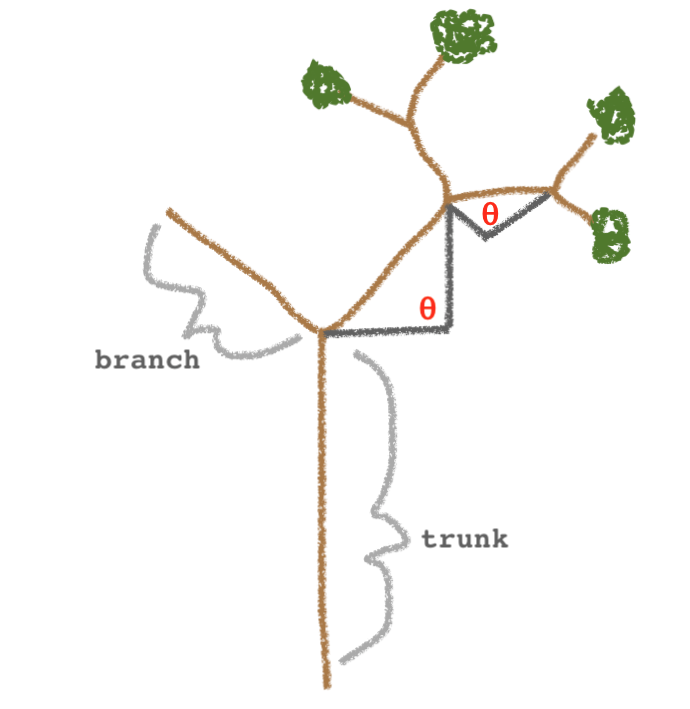
The sketch above shows the basic design of the fractal tree we’ll be creating as an R6 object; let’s unpack it. We’ll have a vertical line as the trunk, and a series of branch lines that recursively sprout two at a time. Lastly, each child branch will have the same angle relative to its parent branch.

Let’s translate the sketch into the object structure that we’ll be using.

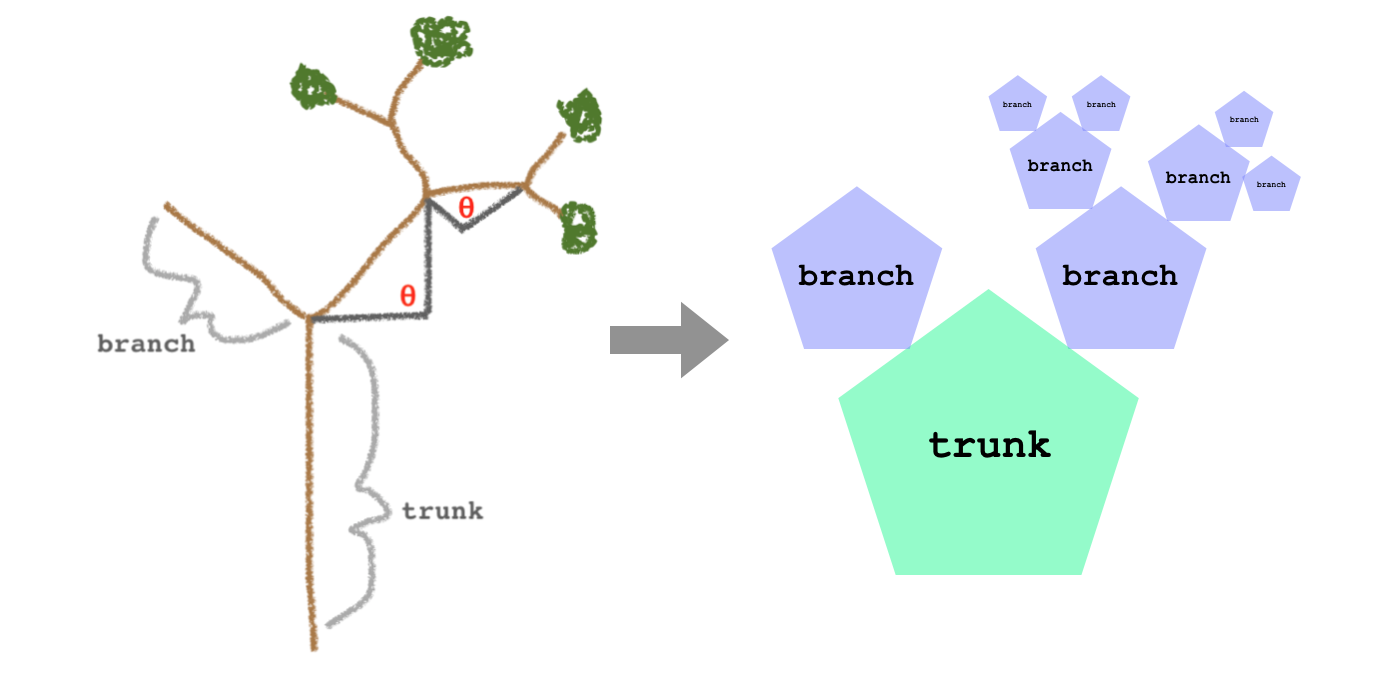
The way it’s drawn up, we see that we’ll be using two separate classes for the trunk and branches. The trunk and branches have a lot in common, so we’ll be using the OOP concept of inheritance as implemented by R6. Below shows how we’ll implement the trunk and branch classes using a base class and inheritance to stay DRY.

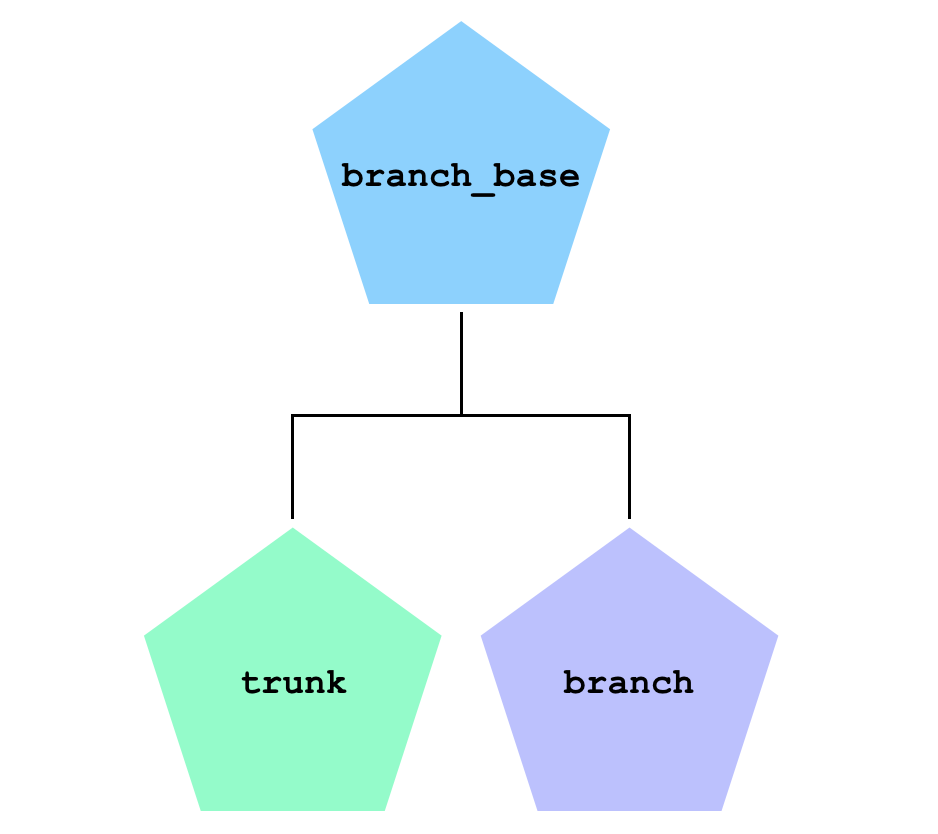
Implementation

We’ll be starting in reverse order of how things were laid out in the design section. The code will be broken out into different sections for easier digestion. If you want to see all the code in one place you can view it here.

branch_base

The branch_base class will be the shared parent of our trunk & branch classes. So we want to pack it full of bits that they’ll share. From an implementation standpoint, what they share is how they’re going to be plotted by ggplot2. Each attribute that is initialized in public is an attribute that will be used to our plot method. Additionally, we use the active feature that will build a data.frame on the fly to represent our branches. Functions that are placed in active can be accessed as if they’re static attributes.

branch_base = R6Class('branch_base',
                      public = list(
                        start_x = NA_integer_,
                        start_y = NA_integer_,
                        end_x = NA_integer_,
                        end_y = NA_integer_,
                        type = NA_character_,
                        id = NA_character_,
                        color = NA_character_
                        ),  # public
                        
                      active = list(
                        df = function() {
                          x = c(self$start_x, self$end_x)
                          y = c(self$start_y, self$end_y)
                          
                          data.frame(x = x, y = y, 
                                     type = self$type, 
                                     id = self$id,
                                     branch_color = self$color)
                          }
                        )  # active
                      )  # branch_base

trunk

The trunk class inherits from branch_base, so we don’t have to think about initializing our attributes or redefining active. To define the class, we add an initialize method that will be used to actually create instances of trunk.

trunk = R6Class('trunk',
                inherit = branch_base,
                public = list(
                  initialize = function(len = 10, branch_color = '#000000') {
                    self$start_x = 0
                    self$start_y = 0
                    self$end_x = 0
                    self$end_y = len
                    self$type = 'trunk'
                    self$branch_color = branch_color
                    
                    self$id = uuid::UUIDgenerate()
                    }
                  )  # public 
                )  # trunk

branch

The definition of branch is similar to trunk, but a little more involved. When we need to create a branch, the info that we’ll be given is where it should start, what direction it should go in, and how long it should be. With these bits of information, we can use some trig to get the branch’s endpoint. The rest of the initialize method is very similar to trunk.

branch = R6Class('branch',
                 inherit = branch_base,
                 public = list(
                   initialize = function(x, y, len = 5, theta = 45, 
                                         type = NA_character_, 
                                         branch_color='#000000') {
                     dy = sin(theta) * len
                     dx = cos(theta) * len
                     
                     self$start_x = x
                     self$start_y = y
                     self$end_x = x + dx
                     self$end_y = y + dy
                     
                     self$type = type
                     self$id = uuid::UUIDgenerate()
                     self$branch_color = branch_color
                     }
                   )  # public
                 )  # branch

fractal_tree

With trunk and branch defined we have the building blocks for our fractal_tree class. This class definition is going to be broken up into sections due to its length/complexity; the full definition can be seen here.

public

The public section of fractal_tree consists of the functionality we need to create and plot our tree.

The initialize method creates all the branches of our tree including the trunk. The private$grow_branches method is a recursive private method of our class that we’ll define soon.

The remaining public method is plot, which, unsurprisingly, will plot our tree. The contents of this method should look fairly familiar to those who are familiar with ggplot2. Thanks to our set up we are able to plot our tree with relatively little effort.

public = list(
  delta_angle = NA_real_,
  len_decay = NA_real_,
  min_len = NA_real_,
  branch_left_color = NA_character_,
  branch_right_color = NA_character_,
  branches = data.frame(),
  
  initialize = function(trunk_len = 10,
                        delta_angle = pi / 8,
                        len_decay = 0.7,
                        min_len = 0.25,
                        trunk_color = '#000000',
                        branch_left_color = '#000000',
                        branch_right_color = '#adadad') {
    self$delta_angle = delta_angle
    self$len_decay = len_decay
    self$min_len = min_len
    self$branch_left_color = branch_left_color
    self$branch_right_color = branch_right_color
    
    self$branches = trunk$new(trunk_len, trunk_color)$df
    
    private$grow_branches(0, trunk_len,
                          len = trunk_len * len_decay,
                          angle_in = pi / 2)
  },
  
  plot = function() {
    ggplot(tree$branches, aes(x, y, group = id, color=branch_color)) +
      geom_line() +
      geom_point(color = 'darkgreen', size=0.5) +
      scale_color_identity() +
      guides(color = FALSE, linetype = FALSE) +
      theme_void()
  }
), # public

private

Our private section consists of a single method, grow_branches. This method will recursively build out our tree forever if given a starting point and an angle. To avoid infinite recursion we’ve built in the min_len attribute that will serve as a stopping point.

The body of the function consists of:

Creating 2 new branches that branch off to the left and right
Adding these branches to the branches attribute (the way this data.frame is dynamically grown could be re-written to be more efficient)
Repeating the process for the left branch (this recursively creates the entire left side of the tree)
Repeating the process for the right branch (this recursively creates the entire right side of the tree)

And that’s it! We now finally have all the pieces in place to create and plot a fractal_tree with R6 and ggplot2.

private = list(
  grow_branches = function(start_x, start_y, 
                           len = 1,
                           angle_in = pi / 2,
                           parent_type = NA, 
                           parent_color = NA) {
    if (len >= self$min_len) {
      l_type = if (!is.na(parent_type)) parent_type else 'left'
      r_type = if (!is.na(parent_type)) parent_type else 'right'
      l_color = if (!is.na(parent_color)) parent_color else self$branch_left_color
      r_color = if (!is.na(parent_color)) parent_color else self$branch_right_color
      
      branch_left  = branch$new(start_x, start_y, len, angle_in + self$delta_angle, l_type, l_color)
      branch_right = branch$new(start_x, start_y, len, angle_in - self$delta_angle, r_type, r_color)
      
      self$branches = rbind(self$branches,
                            branch_left$df,
                            branch_right$df)
      
      private$grow_branches(branch_left$end_x, 
                            branch_left$end_y,
                            angle_in = angle_in + self$delta_angle,
                            len = len * self$len_decay,
                            parent_type = branch_left$type,
                            parent_color = branch_left$branch_color)
      
      private$grow_branches(branch_right$end_x, 
                            branch_right$end_y,
                            angle_in = angle_in - self$delta_angle,
                            len = len * self$len_decay,
                            parent_type =  branch_right$type,
                            parent_color = branch_right$branch_color)
    }
  }  # grow_branches
)  # private

Final Product

This last section will be a few examples of using the functionality of our fractal_tree class.

# Create & plot R6 tree object
tree = fractal_tree$new()
tree$plot()

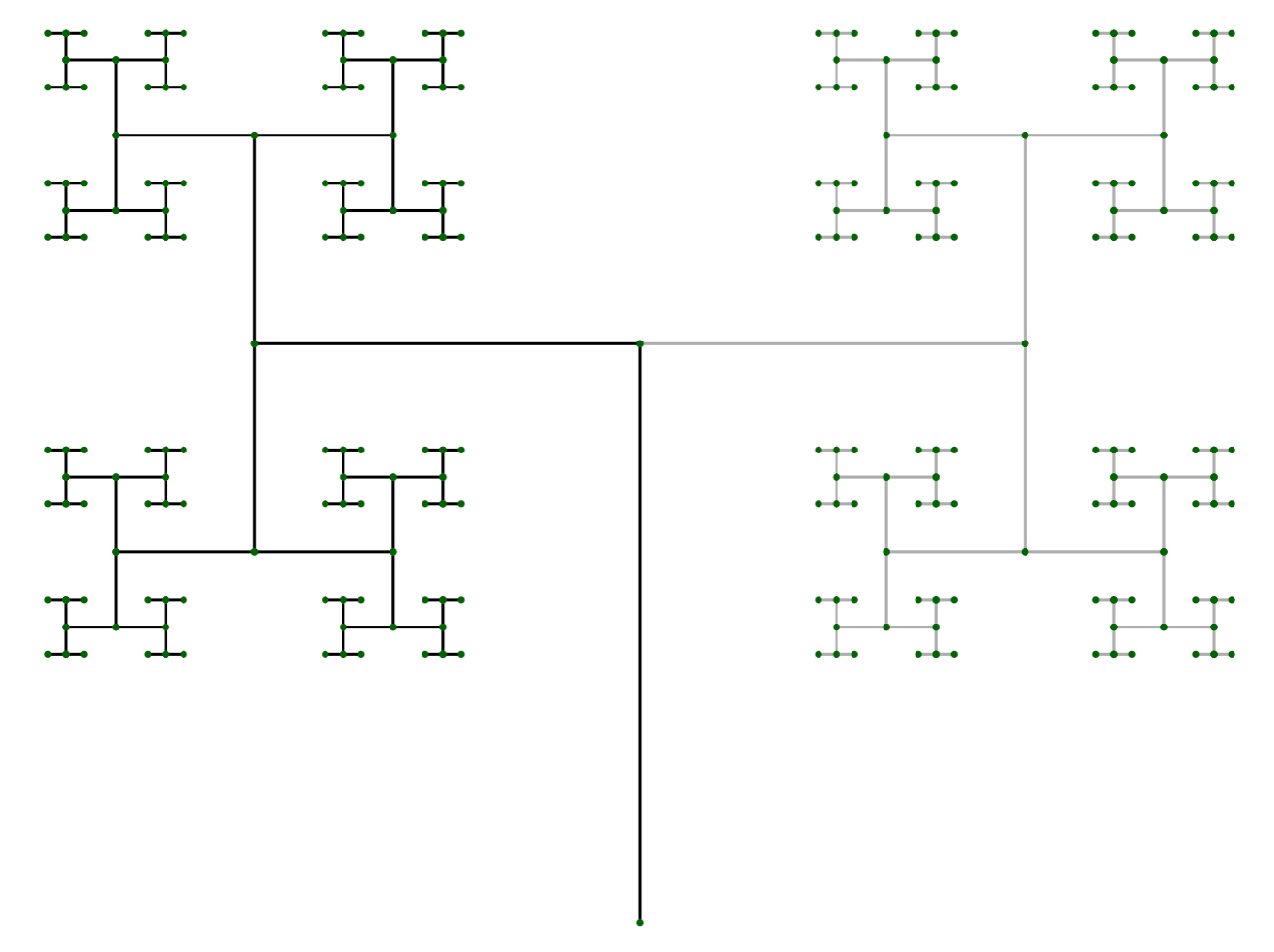
# Create & plot R6 tree object with new angle
tree = fractal_tree$new(delta_angle = pi / 3)
tree$plot()

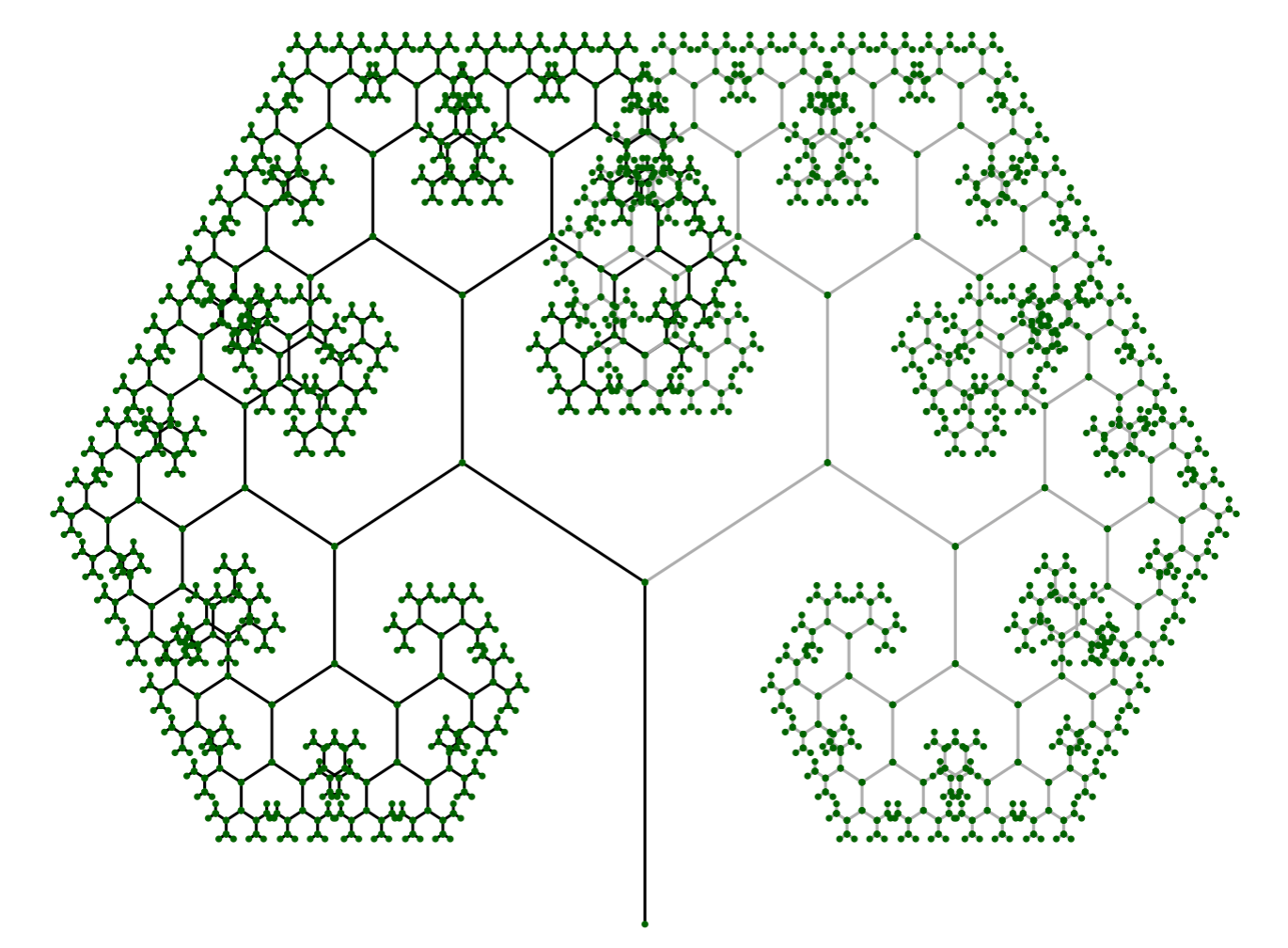
# Create & plot R6 tree object with new branch length decay
tree = fractal_tree$new(delta_angle = pi / 2,
                        len_decay = 0.6)
tree$plot()

# Create & plot R6 tree object with new color
tree = fractal_tree$new(trunk_color = 'tan4', 
                        branch_left_color = 'tan3',
                        branch_right_color = 'tan')
tree$plot()

Adam Spannbauer

OOP Fractal Trees in R with R6, ggplot2, & gganimate (part 1)

Share